Remaining useful lifetime

Dataset

The dataset includes data generated by the “Commercial Modular Aero-Propulsion System Simulation” (C-MAPSS) program. The program was used to simulate the behavior of turbofan engine sensors under various flight conditions until failure. The flight conditions represent situations during ascent and descent to a standard flight altitude of about 10 km.

The C-MAPSS dataset consists of four subsets of data. Each subset contains readings from 21 sensors located in different parts of the degrading engine, controlled by three operational settings characteristics: height, speed, and acceleration in terms of altitude, Mach number, and throttle resolver angle.

Task

The Remain useful lifetime (RUL) prediction problem is the main formulation of the C-MAPSS dataset [1] problem, where the Remain useful lifetime characterizes the remaining length of the degradation trajectory. Because of the weak distinguishability of the healthy state, a piece-wise RUL is commonly used as the target function. The state is considered healthy above the number RUL equal to the specific value \(V\), and the regression model should return there \(V\) as RUL prediction:

\[\begin{split}\begin{equation} RUL=\begin{cases} V, & \text{if $RUL \geq V$}\\ RUL, & \text{if $RUL < V$}. \end{cases} \end{equation}\end{split}\]

Where \(V\) is an heuristic parameter, and in most cases for the C-MAPSS dataset \(V = 125\) value is used due to previously performed empirical study [2]. The piece-wise RUL example is presented in Fig. 1.

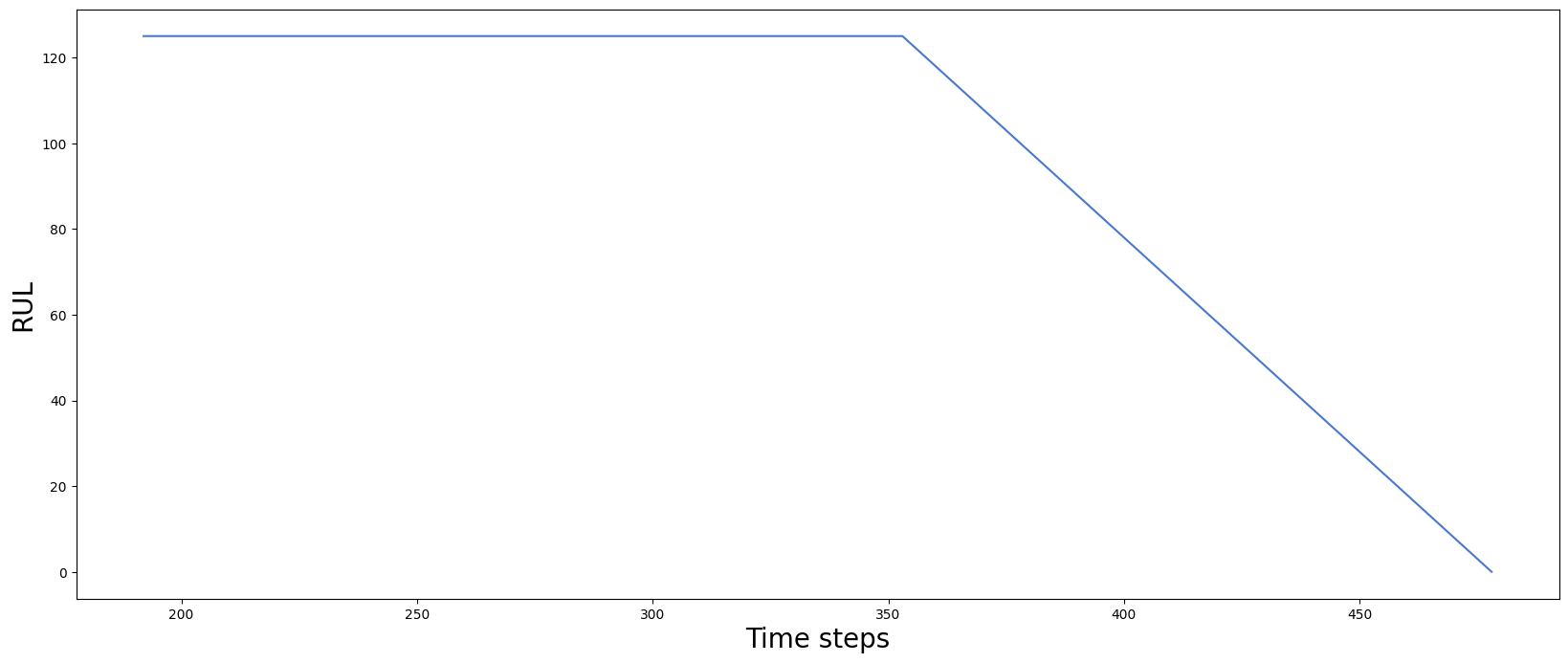
Figure 1: C-MAPSS dataset target example.

Metrics

The model performance on the C-MAPSS dataset RUL problem was evaluated using RMSE and Score metric on the original test dataset. Score and RMSE metrics are:

\[\begin{split}\begin{equation} \begin{aligned} \text{Score} &= \sum_{i=1}^{N} \begin{cases} e^{-\frac{\hat{y}_i - y_i}{13}} - 1, & \text{if } \hat{y}_i - y_i < 0 \\ e^{\frac{\hat{y}_i - y_i}{10}} - 1, & \text{if } \hat{y}_i - y_i \geq 0 \end{cases} \\ \end{aligned} \end{equation}\end{split}\]

\[\begin{equation} RMSE = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2} \end{equation}\]

where \(\hat{y}_i\) and \(y_i\) are predicted and true value of RUL for engine \(i\), \(N\) is number of test samples. The asymmetric Score metric presented in the original paper for PHM2008 competition penalizes overestimations in predictions due to maintenance regulations.

References

The reference results of state-of-the-art papers for the original [1] dataset are presented in table 1.

Table 1: References for C-MAPSS dataset

	FD001		FD003		FD002		FD004
	RMSE | Score		RMSE | Score		RMSE | Score		RMSE | Score
GNMR (2020) [3]	12.14	212	13.23	370	20.85	3196	21.32	2795
BLS-TFCN (2021) [4]	12.08	243	11.43	244	16.87	1605	18.12	2096
TCNN-Transformer (2021) [5]	11.40	254	11.35	415	14.75	1453	17.30	2583
RVE (2022) [6]	13.42	323	12.51	256	14.92	1379	16.37	1846
BiGRU-TSAM (2022) [7]	12.56	213	12.45	232	18.94	2264	20.47	3610
MCA-BGRU (2022) [8]	12.44	211	–	–	–	–	–	–
KGHM (2023) [9]	13.18	251	13.64	333	13.25	1131	19.96	3356
DA-TCN (2021) [10]	11.78 \(\pm\) 0.29	229 \(\pm\) 8	11.56 \(\pm\) 0.61	257 \(\pm\) 58	19.95 \(\pm\) 0.76	1842 \(\pm\) 522	18.23 \(\pm\) 1.06	2317 \(\pm\) 655
ADL-DNN (2022) [11]	13.05 \(\pm\) 0.16	238 \(\pm\) 5	12.59 \(\pm\) 0.25	281 \(\pm\) 5	17.33 \(\pm\) 0.51	1149 \(\pm\) 212	16.95 \(\pm\) 0.44	1371 \(\pm\) 96

[1] Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage propagation modeling for aircraft engine run-to-failure simulation. 2008 international conference on prognostics and health management. 2008; pp 1–9.

[2] Heimes, F. O. Recurrent neural networks for remaining useful life estimation. 2008 International135 Conference on Prognostics and Health Management 2008, 1–6.

[3] Jyoti, N.; Pankaj, M.; Vishnu, T.; Lovekesh, V.; Gautam, S. Graph Neural Networks for Leveraging Industrial Equipment Structure: An application to Remaining Useful Life Estimation. arXiv preprint arXiv:2006.16556v1 2020,

[4] Yu, K.; Wang, D.; Li, H. A Prediction Model for Remaining Useful Life of Turbofan Engines by140 Fusing Broad Learning System and Temporal Convolutional Network. 2021 8th International Conference on Information, Cybernetics, and Computational Social Systems (ICCSS). 2021; pp 137–142.

[5] Wang, H.-K.; Cheng, Y.; Song, K. Remaining Useful Life Estimation of Aircraft Engines Using a Joint Deep Learning Model Based on TCNN and Transformer. Computational Intelligence and145 Neuroscience 2021, 2021.

[6] Costa, N.; Sánchez, L. Variational encoding approach for interpretable assessment of remaining useful life estimation. Reliability Engineering & System Safety 2022, 222, 108353.

[7] Zhang, J.; Jiang, Y.; Wu, S.; Li, X.; Luo, H.; Yin, S. Prediction of remaining useful life based on bidirectional gated recurrent unit with temporal self-attention mechanism. Reliability Engineering150 & System Safety 2022, 221, 108297.

[8] Kara, A. Multi-scale deep neural network approach with attention mechanism for remaining useful life estimation. Computers & Industrial Engineering 2022, 169, 108211.

[9] Li, Y.; Chen, Y.; Hu, Z.; Zhang, H. Remaining useful life prediction of aero-engine enabled by fusing knowledge and deep learning models. Reliability Engineering & System Safety 2023, 229, 108869.

[10] Song, Y.; Gao, S.; Li, Y.; Jia, L.; Li, Q.; Pang, F. Distributed Attention-Based Temporal Convolutional Network for Remaining Useful Life Prediction. IEEE Internet of Things Journal 2021, 8, 9594–9602.

[11] Xiang, S.; Qin, Y.; Liu, F.; Gryllias, K. Automatic multi-differential deep learning and its application to machine remaining useful life prediction. Reliability Engineering & System Safety 2022, 223,108531.